Typenübersicht hydrostatische Sensoren
| Technische Daten | Wert | Einheit |
|---|---|---|
| Messbereich | 200, 500, 1000 | mm |
| Überlastsicher bis | 350 | mBar |
| Power Supply | 12 – 24 | VDC |
| Ausgangssignal | 4-20 mA/Modbus RS 485 | mA/V |
| Nullpunktfehler |
max. ±0,1 % FS
|
% |
| Nichtlinearität [analog] |
± 0,15 % FS
|
% |
| Nichtlinearität [digital] |
± 0,09 % FS
|
% |
| Schockfestigkeit | 100 | G |
| Grenztemp. |
-20°C … +80 °C
|
°C |
| Schutzart | IP65 nach DIN VDE 0470 | |
| Strom | 20 | mA |
Einsatzgebiet: hochpräzise Messung von Vertikalbewegungen
siehe Datenblatt
TYP: PC-HSD4_INK
| Technische Daten | Wert | Einheit |
|---|---|---|
| Messbereich [SW-Sensor] | 500 | mm |
| Messbereich [INK-Sensor] | ± 15 ° | ° |
| Nullpunktfehler [SW-Sensor] | max. ±0,01 % FS | % |
| Nichtlinearität [SW-Sensor] | ± 0,04 % FS | % |
| Nullpunktfehler [INK-Sensor] |
max. ±0,1
|
mm/m |
| Nichtlinearität [digital] |
± 0,2
|
mm/m |
| Auflösung: [INK] | 0,0001° | ° |
| Kommunikation | Modbus ASCII RS485 | |
| Schutzart | IP65 nach DIN VDE 0470 | |
| Strom | 20 | mA |
Einsatzgebiet: hochpräzise Messung von Vertikalbewegungen und Neigungen
Auf Anfrage……
TYP: PC-HSD4 -UA [Ultra Accuracy]
| Technische Daten | Wert | Einheit |
|---|---|---|
| Messbereich | 200, 500, 1000 | mm |
| Überlastsicher bis | 350 | mBar |
| Power Supply | 12 – 24 | VDC |
| Ausgangssignal | Modbus RS 485 | mA/V |
| Nullpunktfehler |
max. ±0,031 % FS
|
% |
| Nichtlinearität [digital] |
± 0,03 % FS
|
% |
| Schockfestigkeit | 100 | G |
| Grenztemp. |
-20°C … +80 °C
|
°C |
| Schutzart | IP65 nach DIN VDE 0470 | |
| Strom | 9 | mA |
Einsatzgebiet: hochpräzise Messung von Vertikalbewegungen ideal für verkehrsbelastete Bauwerke.Interne hochfrequente Abtastung 80 sampels/sec, mit nachgeschalteten frei wählbaren Tiefpassfiltern.
Im Unterschied zu den HSD4 Typen, hat dieser Sensor eine komplett neue Auswerteelektronik on Board. Der Sensor wird intern mit einer Samplingfrequenz von 80 HZ in Verbindung mit einem Tiefpassfilter betrieben. Der Sensor ist speziell für Anforderung in Verbindung mit Bauwerkmonitoring an befahrenen Bücken und sonstigen stark schwingungsbelasteten Infrastrukturen vorgesehen.Im Unterschied zu den HSD4 Typen, hat dieser Sensor eine komplett neue Auswerteelektronik on Board. Der Sensor wird intern mit einer Samplingfrequenz von 80 HZ in Verbindung mit einem Tiefpassfilter betrieben. Der Sensor ist speziell für Anforderung in Verbindung mit Bauwerkmonitoring an befahrenen Bücken und sonstigen stark schwingungsbelasteten Infrastrukturen vorgesehen.Modbus Protokoll Beschreibung
Sensor: Typ HSA2

Datasheet HSA2
TYP: PC-HSA2Einsatzgebiet: hochpräzise Messung von Vertikalbewegungen
| Technische Daten | Wert | Einheit |
|---|---|---|
| Messbereich | 500 | mm |
| Überlastsicher bis | 350 | mBar |
| Power Supply | 12 – 24 | VDC |
| Ausgangssignal | Modbus RS 485 | ASCII |
| Nullpunktfehler |
max. ±0,2 % FS
|
% |
| Nichtlinearität [analog] |
± 0,11 % FS
|
% |
| Nichtlinearität [digital] |
± 0,09 % FS
|
% |
| Schockfestigkeit | 100 | G |
| Grenztemp. |
-20°C … +80 °C
|
°C |
| Schutzart | IP65 nach DIN VDE 0470 |
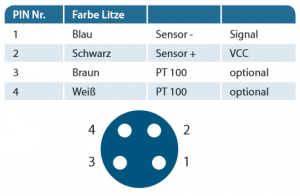
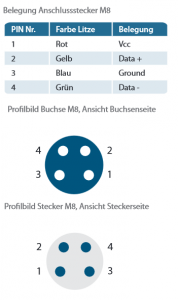
Sensor: Typ HSA6

Datasheet HSA6
TYP: PC-HSA6
| Technische Daten | Wert | Einheit |
|---|---|---|
| Messbereich | 200, 500, 1000 | mm |
| Überlastsicher bis | 350 | mBar |
| Power Supply | 12 – 24 | VDC |
| Ausgangssignal | 4-20 mA/0-5 Volt/RS485 | mA/V |
| Nullpunktfehler |
max. ±0,10% FS
|
% |
| Nichtlinearität |
± 0,09 % FS
|
% |
| Schockfestigkeit | 100 | G |
| Grenztemp. |
-20°C … +80 °C
|
°C |
| Schutzart | IP65 nach DIN VDE 0470 | |
| Strom | 20 | mA |
Einsatzgebiet: hochpräzise Messung von Vertikalbewegungen

Sensor: Typ HSA5

Datasheet HSA5
TYP: PC-HSA5
| Technische Daten | Wert | Einheit |
|---|---|---|
| Messbereich | 200, 500, 1000 | mm |
| Überlastsicher bis | 350 | mBar |
| Power Supply | 12 – 24 | VDC |
| Ausgangssignal | 4-20 mA/0-5 Volt/RS 485 | mA/V |
| Nullpunktfehler |
max. ±0,09 % FS
|
% |
| Nichtlinearität |
± 0,08 % FS
|
% |
| Schockfestigkeit | 100 | G |
| Grenztemp. |
-20°C … +80 °C
|
°C |
| Schutzart | IP65 nach DIN VDE 0470 | |
| Strom | 20 | mA |
Einsatzgebiet: hochpräzise Messung von Vertikalbewegungen

Sensor: Typ HSA7

TYP: PC-HSA7
| Technische Daten | Wert | Einheit |
|---|---|---|
| Messbereich | 200, 500, 1000 | mm |
| Überlastsicher bis | 350 | mBar |
| Power Supply | 12 – 24 | VDC |
| Ausgangssignal | Digital RS 485 | ASCII |
| Nullpunktfehler |
max. ±0,05 % FS
|
% |
| Nichtlinearität |
± 0,06 % FS
|
% |
| Schockfestigkeit | 200 | G |
| Grenztemp. |
-20°C … +80 °C
|
°C |
| Schutzart | IP65 nach DIN VDE 0470 | |
| Strom | 50 | mA |
Einsatzgebiet: hochpräzise Messung von Vertikalbewegungen
Deformationsanalyse an einem Turbinentisch, hier können Sie die Ergebnisse einer Verformungsmessung an einem Turbinentisch sehen. Die Messung fand während einer An- bzw. Abfahrt der Turbine statt. Solche Messungen sind nur mit dem Sensortyp HSA7 und der entsprechenden Software „POCO-Analyzer“ möglich. Das einzige Verfahren seiner Art, um solche geometrischen Veränderung während des Betriebes der Turbine zu messen. Ein entscheidender Punkt ist hier, die Berechnung von Ausgleichsebenen, auf Grundlage der iterativen Ist- und Sollwertanpassung der ermittelten Vertikalbewegungen (iterated closest point).
Das Iterative Closest Point (ICP)-Verfahren ist ein iterativer Algorithmus zur Registrierung und Ausrichtung von Punktwolken in der 3D-Datenverarbeitung. Ziel ist es, eine optimale Transformation (bestehend aus Rotation und Translation) zu bestimmen, die eine Quell-Punktwolke an eine Ziel-Punktwolke anpasst, um eine möglichst genaue Überlagerung zu erreichen.
Der Algorithmus basiert auf den folgenden Schritten:
- Initialisierung: Eine Anfangsschätzung für die Transformation wird festgelegt, um die Punktwolken in eine grobe Übereinstimmung zu bringen.
- Zuordnung der Punkte: Für jeden Punkt in der Quell-Punktwolke wird der nächstgelegene Punkt in der Ziel-Punktwolke ermittelt. Diese Zuordnungen bilden die Korrespondenzpaare.
- Berechnung der optimalen Transformation: Unter Verwendung der Korrespondenzpaare wird eine Transformation (Rotation und Translation) berechnet, die die Summe der quadrierten Abstände zwischen den korrespondierenden Punkten minimiert. Dies erfolgt häufig durch die Lösung eines Procrustes-Problems mittels Singular Value Decomposition (SVD).
- Transformation der Quell-Punktwolke: Die berechnete Transformation wird auf die Quell-Punktwolke angewandt.
- Iteration: Die Schritte 2 bis 4 werden wiederholt, bis eine Abbruchbedingung erfüllt ist, beispielsweise wenn die Veränderung der Transformation zwischen aufeinanderfolgenden Iterationen unter einen vordefinierten Schwellenwert fällt oder eine maximale Anzahl an Iterationen erreicht ist.
Notwendige numerischen Stabilität und an den Einzelfall angepasste Algorithmen dienen exakten Berechnung der tatsächlich vorhandenen Deformationen.


